Markovmodellen

Senast uppdaterad: 2025-08-20

Markovmodellen är ett en matematisk modell som används för att beskriva hur en variabel förändras mellan olika stadier över tid. Inom hälsoekonomi används modellen för att simulera hur patienter rör sig mellan olika hälsotillstånd över tid, till exempel från frisk till sjuk eller från sjuk till död.

Markovmodellen bygger på att sannolikheten för ett framtida tillstånd bara beror på det nuvarande tillståndet, inte på tidigare historik. Modellen delas upp i cykler, och i varje cykelcykel: beräknas sannolikheten för att en individ antingen stannar kvar i sitt tillstånd eller övergår till ett annat. Varje tillstånd kallas Markovtillstånd, och förändringarna mellan dessa kallas övergångssannolikheter.

Modellen är särskilt användbar vid kroniska sjukdomar eller långvariga behandlingar där patientens tillstånd kan förändras gradvis. Genom att kombinera sannolikheter, kostnader och hälsoeffekter i varje tillstånd kan man räkna ut den totala kostnaden och nyttan av olika behandlingsalternativ.

Övergångssannolikheterna som används i en Markovmodell hämtas ofta från kliniska studier, observationsdata, register eller metaanalyser. Ibland kan de också baseras på expertbedömningar om det saknas tillräcklig data. För varje cykelcykel: beräknas sannolikheten att gå från ett tillstånd till ett annat. För att säkerställa att modellen ger rimliga resultatresultat: jämförs modellens prediktioner med faktiska utfall från kliniska studier eller patientregister. Detta kallas ibland extern validering. Eftersom det alltid finns osäkerhet i skattade sannolikheter görs även känslighetsanalyser. Det innebär att man testar hur ”stabila” resultaten är när vissa förutsättningar, data och antaganden ändras.

Markovmodell – ett exempel:

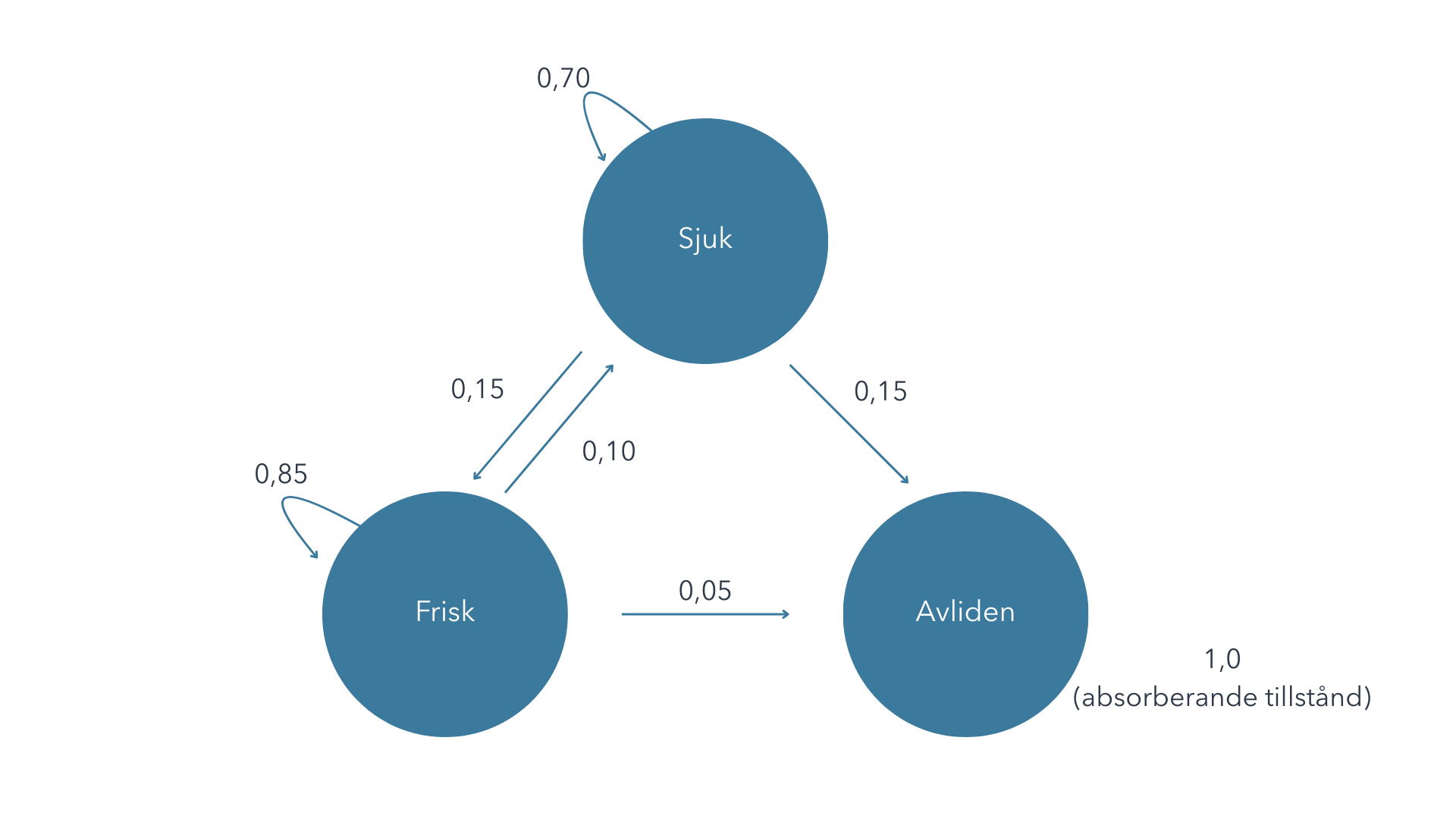
Element i en Markovmodell:

• Markovtillstånd: I denna exempelmodell är tillstånden frisk, sjuk och död. De representeras av de blå cirklarna.
• Övergångssannolikhet: Siffrorna visar sannolikheten att gå från ett tillstånd till ett annat. Till exempel 0,10 i denna modell betyder att det är tio procents sannolikhet att gå från att vara frisk till att vara sjuk under en cykelcykel:.
• Absorberande tillstånd: När man når detta tillstånd kan man inte lämna det, därför är sannolikheten att stanna kvar 1,0 (100 procent).
• Sannolikheten att stanna kvar i samma tillstånd: De bågformade pilarna visar sannolikheten att förbli i det aktuella tillståndet under en cykelcykel:, till exempel att förbli frisk eller fortsatt sjuk.

Trots att Markovmodellen är användbar inom hälsoekonomiska analyser har de vissa begränsningar. Modellen utgår ofta från att alla individer har samma risk att byta tillstånd, oavsett bakgrund eller tidigare tillstånd, vilket inte alltid speglar verkligheten. Den antar ofta även att riskerna är konstanta över tid. Dessa förenklingar kan ibland hanteras genom att lägga till fler tillstånd eller använda mer avancerade modeller, som individbaserade simuleringar. Det kan dock göra modellerna så komplexa att de blir svåra att genomföra, tolka och kommunicera.