Beslutsträdsmodellen

Senast uppdaterad: 2025-08-15

Beslutsträdsmodellen är ett analysverktyg som används för att strukturera och utvärdera beslutssituationer med ett begränsat antal möjliga utfall och korta tidshorisonter. Modellen visar beslutsalternativ och deras potentiella konsekvenser i en grafisk struktur. Inom hälsoekonomi används beslutsträd för att beräkna förväntande värden baserat på sannolikheter, kostnader och hälsoeffekter.

Den här typen av modeller är vanliga inom hälsoekonomiska utvärderingar, där de används för att jämföra två eller flera beslutsalternativ. Syftet är ofta att avgöra om en ny behandling är kostnadseffektiv. Resultatet uttrycks vanligen i kostnaden per vunnet kvalitetsjusterat levnadsår (QALYQALY:), men det kan också redovisas i termer av rena levnadsår eller i monetära termer. På så vis kopplas beslutsträdsmodellen till kärnan i hälsoekonomi, som ett matematiskt verktyg för att väga kostnader mot hälsoeffekter.

Beslutsträdsmodellen används för att analysera beslut som gäller situationer med ett begränsat antal möjliga utfall och korta tidshorisonter. En fördel är att modellen är särskilt användbara vid sjukdomar som inträffar en gång, till exempel akuta tillstånd, eftersom den gör det möjligt att tydligt strukturera beslutsalternativen och deras konsekvenser. Begränsningar med beslutsträd är att de snabbt kan bli komplexa om det finns många möjliga utfall, att de är mindre lämpliga för långsiktiga analyser, och att de inte är applicerbara på återkommande tillstånd eller kroniska sjukdomar.

Element i ett beslutsträd

• Beslutsnod vid trädets startpunkt.
• Grenarna vid beslutsnoden representerar alternativen som ska jämföras och kallas strategigrenar.
• Sannolikhetsnoder från varje strategigren. Dessa representerar sannolikheten för olika utfall beroende på val av strategi.
• Utfallsnod i slutet av varje gren med olika utfall och dess respektive sannolikheter. Dessa utfall är ömsesidigt uteslutande, det vill säga att man endast kan få ett utfall.

Sannolikheterna för de möjliga utfallen kommer vanligen från publicerade studier. Antingen i form av befintlig data som försöksdata och observationsdata eller genom metaanalys där sannolikheter aggregeras från olika studier. Sannolikheter är tal mellan noll och ett och alla grenar som kommer från en sannolikhetsnod ska summera till ett.

Utfallen av analysen ses vid utfallsnoderna och kan beskrivas med olika mått beroende på studiens syfte. Vanliga utfall inkluderas totala kostnader, total nytta, antalet levnadsår samt kvalitetsjusterade levnadsår (QALYQALY:). Dessa värden hämtas vanligtvis från kliniska studier, registerdata eller tidigare publicerade hälsoekonomiska analyser. Vilket eller vilka mått som används beror på vilken typ av beslutsunderlag som eftersträvas.

Beslutsträdsmodell – ett exempel:

• KostnadKostnad: läkemedel A: 15 000 kr
• KostnadKostnad: läkemedel B: 25 000 kr
• KostnadKostnad: sjuk: 5 000 kr
• Livskvalitet sjuk: 0,6 QALYQALY:

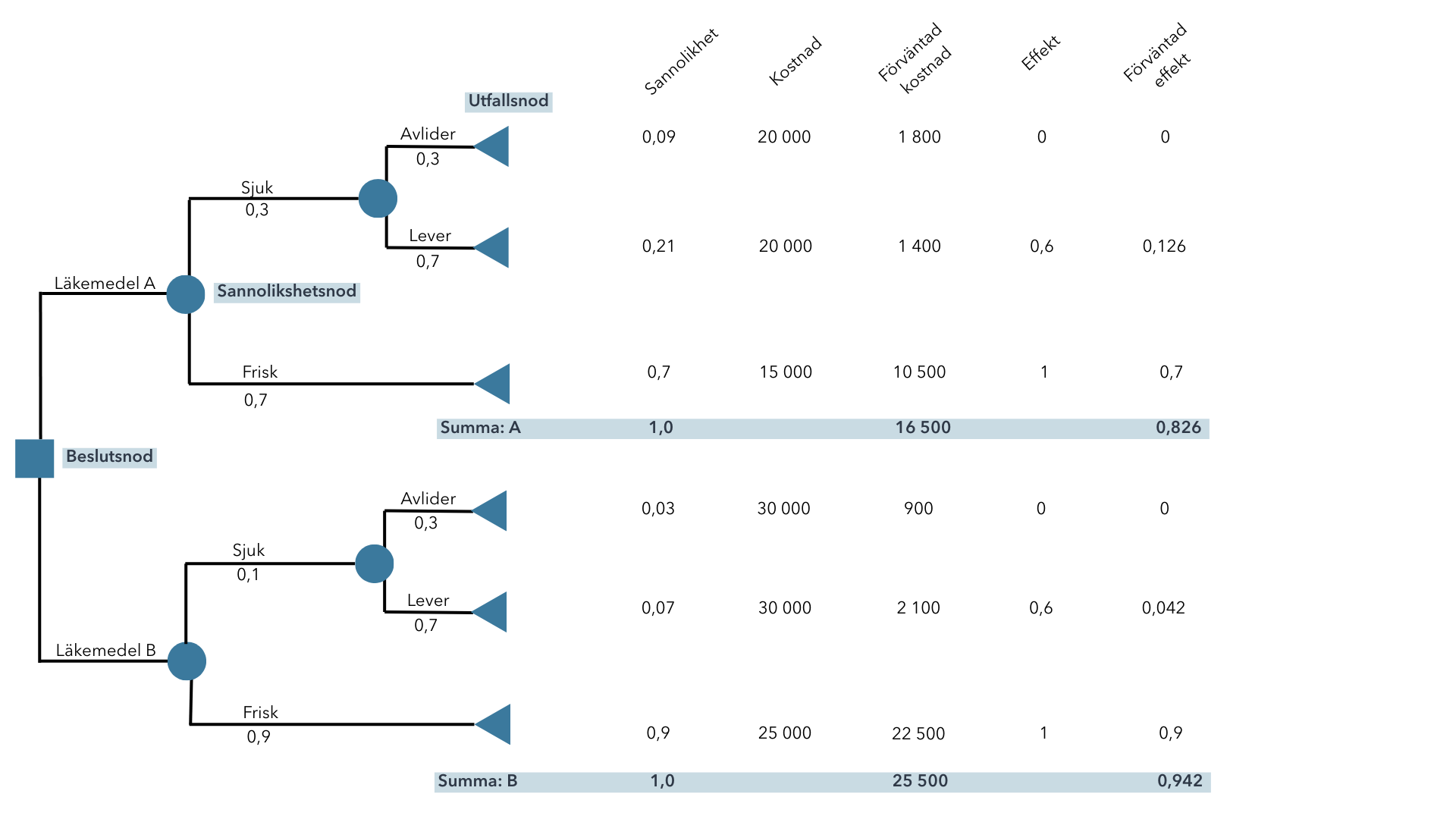
Beräkningar i beslutsträdsmodellen

Nedan följer ett räknexempel för översta raden i exemplet ovan. Övriga beräkningar följer samma mönster.

• Sannolikhet: Produkten av sannolikheterna längs grenen. 0,3 x 0,3 = 0,09
• Kostnad: Läkemedels- och sjukdomskostnad. 15 000 + 5 000 = 20 000
• Förväntad kostnad: Sannolikhet multiplicerat med kostnadkostnad:. 0,09 x 20 000 = 1 800
• Effekt: Livskvaliteten för det aktuella tillståndet. 0 QALY
• Förväntad effekt: Livskvalitet multiplicerat med sannolikhet. 0 x 0,09 = 0

Det mest fördelaktiga alternativet avgörs inte enbart av lägsta kostnadkostnad: eller högsta effekt var för sig, utan av kombinationen av dessa två. För att väga samman kostnadkostnad: och effekt i kostnadseffektivitet används ofta den inkrementella kostnadseffektivitetskvoten (ICERICER:), som anger merkostnaden per vunnen effekt­enhet när man väljer ett alternativ framför ett annat.

I exemplet ovan beräknas ICER enligt följande:

Det betyder att läkemedel B kostar cirka 77 600 kr mer per vunnen QALYQALY: jämfört med läkemedel A.

Resultaten testas sedan med känslighetsanalyser. Känslighetsanalys innebär att man testar hur ”stabila” resultaten är när vissa förutsättningar, data och antaganden ändras.